Simulate mortgages with matplotlib

A mortgage is a type of loan where you borrow money from a bank and agree to pay it back with interest over a period of time. It is commonly used to purchase real state. The inputs to calculate a mortgage are:

• 💵 Amount of money borrowed.
• 📈 Annual interest rate.
• 📅 Years of the mortgage.

The ultimate goal is to determine how much you will have to pay per month during the mortgage term and the total interest paid.

We define a function that calculates the installment and total interest. This function implements the amortization formula.

def calculate_mortgage(loan, interest, years):
    monthly_interest = interest / 1200
    num_payments = years * 12
    installment = (loan * monthly_interest) / (1 - (1 + monthly_interest) ** -num_payments)
    total_interest = ((installment * num_payments - loan) / loan) * 100
    return (installment, total_interest)

Now we can use it with the following parameters:

• 💵 You want to borrow 100,000 Euros.
• 📈 At 2% annual interest.
• 📅 For 10 years.

With this, we can see that the monthly payment is 920 Euros, and the interest is 10%. That is, after 10 years, you will have paid 10% of what you borrowed.

installment, interest = calculate_mortgage(100000, 2, 10)
print(f"Monthly installment: {installment:.2f} €")
print(f"Interest: {interest:.2f} %")
# Monthly installment: 920.13 €.
# Interest: 10.42 %

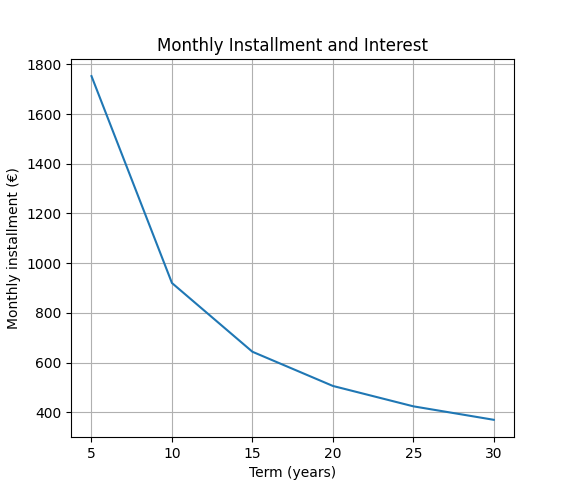
We can calculate this for various terms, from 5 to 30 years.

loan = 100000
interest = 2
terms = range(5, 31, 5)

installments = [calculate_mortgage(loan, interest, term)[0] for term in terms]

fig, ax1 = plt.subplots(figsize=(7, 6))
ax1.set_xlabel("Term (years)")
ax1.set_ylabel("Monthly installment (€)")
ax1.plot(terms, installments, label="Monthly installment (€)")
plt.title("Monthly Installment and Interest")
plt.grid(True)
plt.show()

And we see the monthly payment for each case.

✏️ Exercises:

• As we can see, the monthly payment is reduced considerably when we increase the term of the mortgage. However, this affects the interest paid. Add a graph representing the interest paid and the term in years.